第一講:加算と乗算
1. はじめに
アナデンのダメージ計算では、効果量が加算関係にある場合と乗算関係にある場合があることはご存知の方も多いと思います。
表記上は同じ倍率でも、加算か乗算かによって最終的な倍率に大きな差が出ることがあります。
よくある例としては、属性グラスタ(加算型)と毒・ペイングラスタ(乗算型)でそれぞれ+30%を3つ装備した場合、以下の計算式となります。
| 属性(加算): | \(1 + 0.3 \times 3 = 1.9\) 倍 |
| 毒・ペイン(乗算): | \(1.3^3 = 2.197\) 倍 |
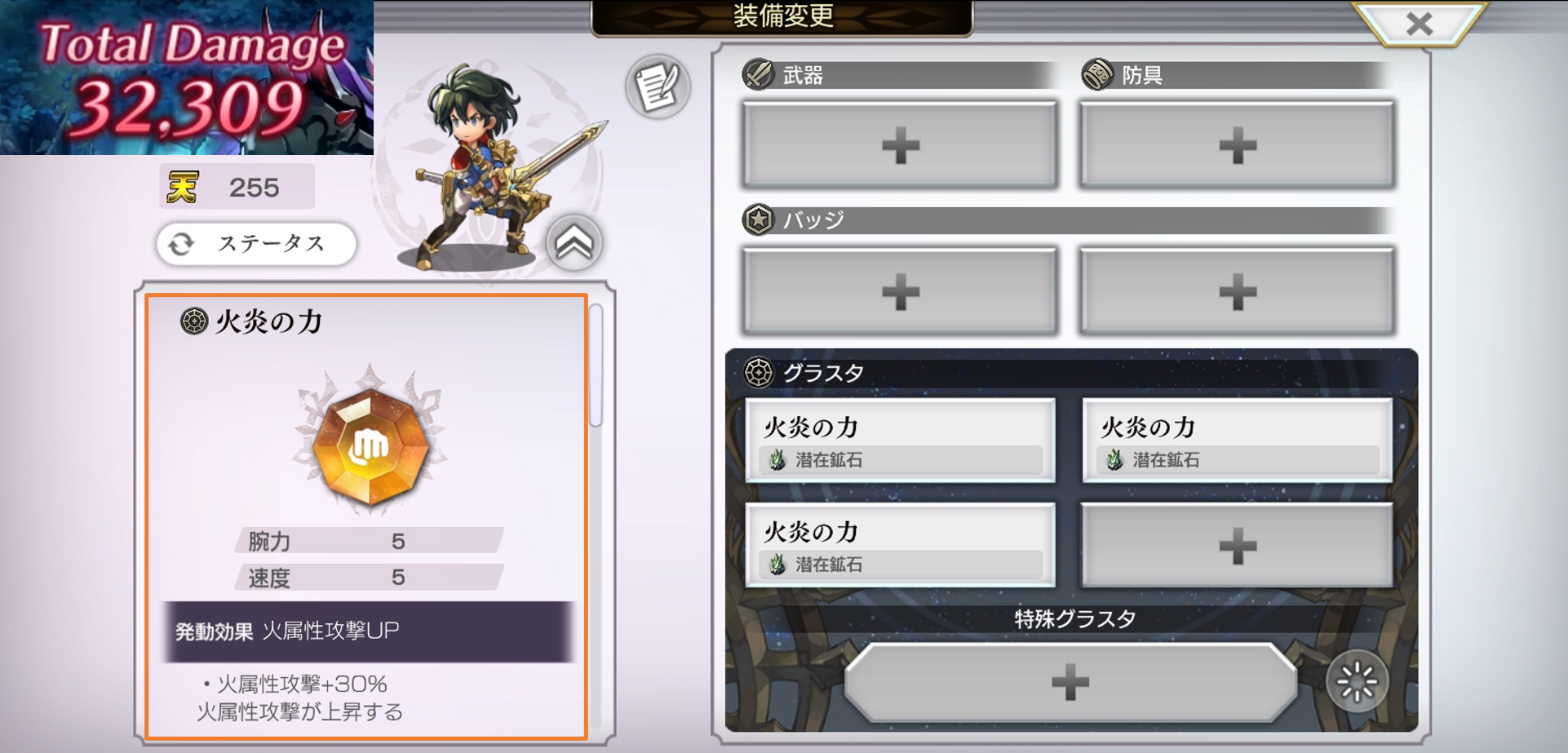
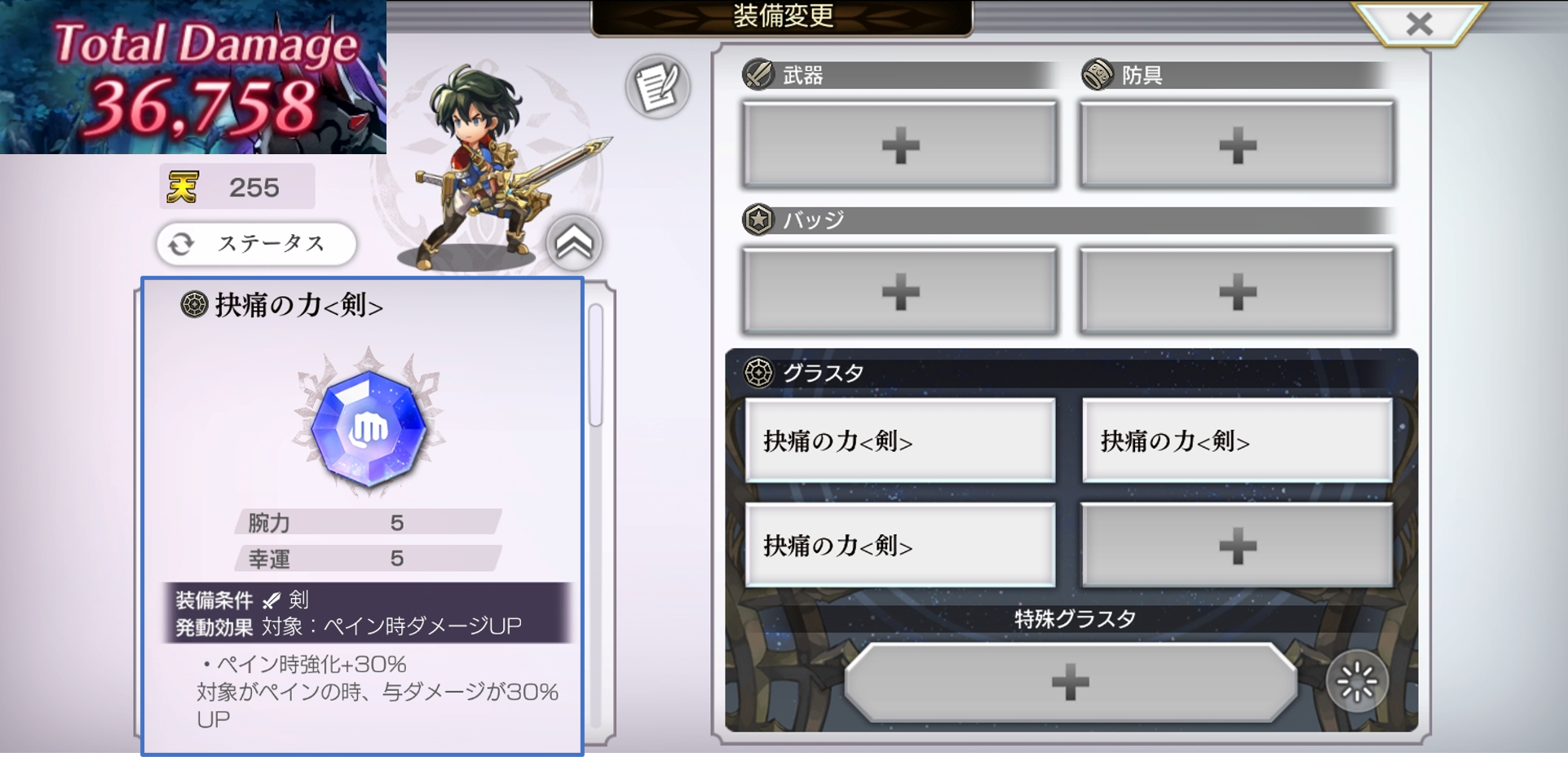
このように、表記は同じでも乗算の方がダメージが大きくなっていることがわかります。感覚的に「乗算のほうが強い」と理解している方も多いと思います。 しかし、先ほど挙げた例はあくまで一例にすぎず、すべての効果量 \(x\) において常に乗算が加算以上となることを説明するものではありません。
そこで本講では、この加算と乗算の大小関係を数学的に一般化することを目指します。
2. 一般化
先ほどの例のように、効果量 \(x \in \mathbb{R}_{>0}\)、効果の個数 \(n \in \mathbb{N}\) において、
| 加算型: | \(1 + n x\) |
| 乗算型: | \((1 + x)^n\) |
と表すことができます。したがって、乗算が加算以上であることを示すには
\begin{equation} (1 + x)^n \ge 1 + nx \tag{1} \end{equation}が常に成り立つことを示せば十分です。
余談ですが、(1)式は一般にベルヌーイの不等式として知られています。 厳密には\(x>-1\) のとき成立すると主張するものですが、ここでは \(x>0\) を仮定しているため条件は満たします。
では実際に(1)式の証明を行ってみます。ここでは帰納法を用います。
【証明】
\(n = 1\) のとき、
\[ \begin{align} \text{左辺} &= (1+x)^1 = 1+x \\ \text{右辺} &= 1+x \end{align} \]
よって、\(n = 1\)のとき与式は成り立つ。
\(n = k\) のとき、与式が成立すると仮定すると、
\[ \begin{align} (1+x)^{k+1} &= (1+x)(1+x)^k \\ &\ge (1+x)(1+kx) \\ &= 1 + (k+1)x + kx^2 \\ &\ge 1 + (k+1)x \end{align} \]
よって、 \(n = k + 1\) においても与式は成り立つ。
以上より、すべての自然数 \(n\) について与式は成り立つ。
3. 不等式の拡張
2節で示した(1)式は、すべての効果量が同じ値 \(x\) の場合に限定したものでした。 しかし、実際にはそれぞれの効果量が異なるケースも当然ながらあります。この場合も一般化できます。
\(n\)の定義は2節と同じとし、効果量 \(x_i \in \mathbb{R}_{>0}\) \((i=1,…,n)\) において、
| 加算型: | \(\displaystyle 1 + \sum_{i=1}^{n} x_i\) |
| 乗算型: | \(\displaystyle \prod_{i=1}^{n} (1 + x_i)\) |
と表すことができます。したがって、乗算が加算以上であることを示すには
\begin{equation} \prod_{i=1}^{n} (1 + x_i) \;\ge\; 1 + \sum_{i=1}^{n} x_i \tag{2} \end{equation}が常に成り立つことを示せば十分です。こちらも帰納法を用いて証明します。
【証明】
\(n=1\) のとき、
\[ \begin{align} \text{左辺} &= \displaystyle \prod_{i=1}^{1} (1+x_i) = 1 + x_1,\\ \text{右辺} &= 1 + \sum_{i=1}^{1} x_i = 1 + x_1 \end{align} \]
よって、\(n=1\) のとき与式は成り立つ。
\(n = k\) のとき、与式が成立すると仮定すると、
\[ \begin{align} \displaystyle \prod_{i=1}^{k+1} (1 + x_i) &= (1 + x_{k+1}) \displaystyle\prod_{i=1}^{k} (1 + x_i) \\ &\ge (1 + x_{k+1})\!\left(1 + \sum_{i=1}^{k} x_i\right) \\ &= 1 + \sum_{i=1}^{k+1} x_i + x_{k+1}\sum_{i=1}^{k} x_i \\ &\ge 1 + \sum_{i=1}^{k+1} x_i \end{align} \]
よって、 \(n=k+1\) においても与式は成り立つ。
以上より、すべての自然数 \(n\) について与式は成り立つ。
【補足:二項定理による証明】
(1)式だけであれば二項定理でも簡単に示せます。\((1+x)^n\) を二項定理により展開すると、
\[ \begin{align} (1+x)^n &= 1 + nx + \frac{n(n-1)}{2}x^2 \\ &\quad + \cdots + x^n \end{align} \]
が得られます。ここで \(x \geq 0\) のとき、二次以上の項 \(\frac{n(n-1)}{2}x^2, \dots\) はすべて 0 以上であることから、
\[ (1+x)^n \geq 1 + nx \]
となり、直ちに(1)式が得られます。上記の様に、非負なる二次以上の交差項によって成り立つことがわかります。
4. まとめ
本講では乗算が常に加算以上となることを確認しました。 このように、乗算の効果を持つ要素を組み合わせたほうがより高い火力を発揮できる、という直感的理解を裏付けることができます。 「ダメージ\(+x\)%」の \(x\) の数字だけで装備の優劣を判断しないことは、グラスタに限らず重要な観点です。
以上です。